AbbildungDefinition Abbildung
Schule
Es seien X und Y zwei beliebige Mengen.
Eine eindeutige Zuordnung der Elemente aus X zu den Elementen aus Y heißt Abbildung.
Bemerkungen
Die Menge X heißt Definitionsbereich und Y Wertebereich.
Eine Funktion ist eine spezielle Abbildung mit dem Wertebereich 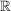 oder oder  . .
Universität
X und Y seien Mengen, 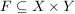 eine Relation eine Relation
Ist F linksvollständig und rechtseindeutig, dann nennt man das Tripel 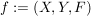 eine Abbildung. eine Abbildung.
Definition aus dem Meyberg:
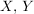 seien Mengen. Ein Tripel seien Mengen. Ein Tripel 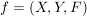 heißt eine Abbildung von heißt eine Abbildung von 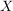 in in 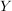 (oder eine Funktion auf (oder eine Funktion auf 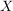 mit Werten in mit Werten in 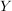 ), wenn gilt: ), wenn gilt:
(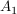 ) ) 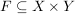
(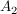 ) Zu jedem ) Zu jedem 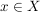 gibt es genau ein gibt es genau ein 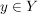 mit mit  . .
 heißt der Graph, heißt der Graph, 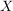 die Quelle oder der Definitionsbereich, die Quelle oder der Definitionsbereich, 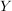 das Ziel oder der Wertevorrat von das Ziel oder der Wertevorrat von 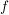 . .
Das durch  eindeutig bestimmte Element eindeutig bestimmte Element 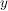 mit mit  wird meist mit wird meist mit 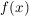 bezeichnet. Also bezeichnet. Also
 . .
Folgende Schreibweisen für eine Abbildung 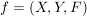 werden verwendet: werden verwendet:
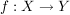 oder oder  , ,
wenn man über  nichts Näheres zu wissen braucht, andernfalls fügt man hinzu nichts Näheres zu wissen braucht, andernfalls fügt man hinzu
 oder oder 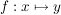 (lies: " (lies: "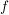 bildet bildet  auf auf 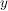 ab"). ab").
Bemerkung:
Die "klassische" Definition einer Abbildung, etwa so "Eine Abbildung 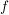 von von 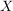 nach nach 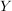 ist eine Vorschrift, die jedem Element ist eine Vorschrift, die jedem Element 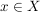 eindeutig ein Element eindeutig ein Element 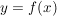 aus aus 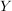 zuordnet", ist natürlich in obiger Definition verarbeitet. Da aber ein Tripel ein besseres mathematisches Objekt ist als eine Vorschrift, zieht man heute die erste Definition vor. Die Vorschrift allerdings bleibt doch in konkreten Fällen erhalten, nämlich in der Beschreibung von zuordnet", ist natürlich in obiger Definition verarbeitet. Da aber ein Tripel ein besseres mathematisches Objekt ist als eine Vorschrift, zieht man heute die erste Definition vor. Die Vorschrift allerdings bleibt doch in konkreten Fällen erhalten, nämlich in der Beschreibung von  . Auch wir werden sehr oft zu prüfen haben, ob eine durch eine gewisse Vorschrift definierte Teilmenge . Auch wir werden sehr oft zu prüfen haben, ob eine durch eine gewisse Vorschrift definierte Teilmenge 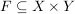 auch wirklich eine Abildung auch wirklich eine Abildung 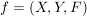 definiert, Dazu muss man prüfen, ob jedes Element von definiert, Dazu muss man prüfen, ob jedes Element von 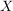 auch als erste Komponente eines Elementes aus auch als erste Komponente eines Elementes aus  vorkommt (das ist meist trivial zu sehen) und, was wichtiger ist, dass vorkommt (das ist meist trivial zu sehen) und, was wichtiger ist, dass  und und 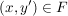 nur für nur für 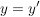 möglich ist. In anderer Schreibweise sieht das so aus: möglich ist. In anderer Schreibweise sieht das so aus:
 . .
Abbildungen 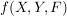 und und 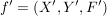 sind genau dann gleich, wenn sind genau dann gleich, wenn 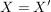 , , 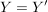 und und 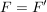 gilt; d.h. wenn Quelle, Ziel und Graph übereinstimmen. Insbesondere gilt; d.h. wenn Quelle, Ziel und Graph übereinstimmen. Insbesondere
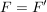
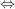 (Für alle (Für alle 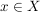 gilt: gilt: 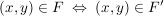 ) )
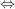 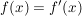 für alle für alle 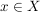 . .
D.h. Abbildungen 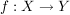 und und 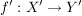 sind genau dann gleich, wenn sind genau dann gleich, wenn 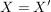 , , 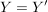 und und 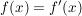 für alle für alle 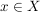 gilt. gilt.
Ist 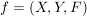 eine Abbildung und eine Abbildung und 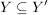 , dann ist offensichtlich , dann ist offensichtlich 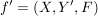 ebenfalls eine Abbildung. Ist ebenfalls eine Abbildung. Ist 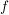 injektiv, so auch injektiv, so auch  . Hingegen ist . Hingegen ist  im Falle im Falle 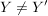 niemals surjektiv, auch wenn niemals surjektiv, auch wenn 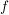 surjektiv ist. Dennoch möchte man zwischen surjektiv ist. Dennoch möchte man zwischen 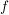 und und  keinen wesentlichen Unterschied machen. Man nennt Abbildungen keinen wesentlichen Unterschied machen. Man nennt Abbildungen 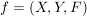 und und 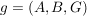 im wesentlichen gleich, wenn im wesentlichen gleich, wenn 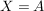 und und  gilt, d.h. gilt, d.h. 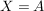 und und 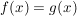 für alle für alle 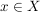 . Wenn Missverständnisse ausgeschlossen sind, schreibt man auch hierfür . Wenn Missverständnisse ausgeschlossen sind, schreibt man auch hierfür 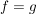 . .
Eine gegebene Abbildung 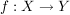 kann man auf Teilmengen von kann man auf Teilmengen von 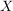 beschränken. Sei beschränken. Sei 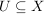 , dann heißt , dann heißt
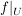 : :  , , 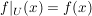 für alle für alle 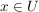 , ,
die Restriktion von 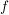 auf auf 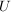 . Es ist . Es ist  nur für nur für 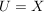 . .
Die Abbildung  , , 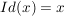 , wird als Identität (auf , wird als Identität (auf 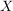 ) bezeichnet. Wenn nötig, schreibt man hierfür auch ) bezeichnet. Wenn nötig, schreibt man hierfür auch  . .
Seien 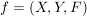 , , 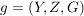 Abbildungen und Abbildungen und  . Man definiert eine Teilmenge . Man definiert eine Teilmenge 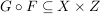 durch durch
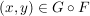 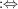  und und 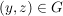 . .
Dann ist 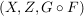 eine Abbildung, da eine Abbildung, da 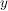 durch durch  und und  durch durch 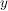 eindeutig bestimmt sind, und somit eindeutig bestimmt sind, und somit  durch durch  eindeutig bestimmt ist. Diese Abbildung wird mit eindeutig bestimmt ist. Diese Abbildung wird mit 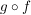 ( (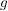 komponiert mit komponiert mit 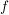 ) bezeichnet und heißt das Kompositum (oder Produkt) von ) bezeichnet und heißt das Kompositum (oder Produkt) von 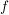 und und 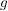 . In anderer Schreibweise sieht das so aus: . In anderer Schreibweise sieht das so aus:
Für 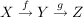 ist ist 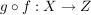 definiert durch definiert durch
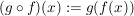 für alle für alle 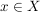 . .
Ist  eine weitere Abbildung, dann gilt: eine weitere Abbildung, dann gilt:
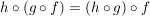 , ,
denn Quelle und Ziel sind gleich und für alle 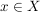 gilt: gilt:
 = h(g(f(x))) = [(h \circ g) \circ f](x) $ $ [h \circ (g \circ f)](x) = h(g(f(x))) = [(h \circ g) \circ f](x) $](/teximg/0/7/00386970.png) . .
Sei 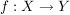 eine Abbildung und eine Abbildung und 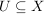 . Die Menge . Die Menge

heißt das 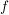 -Bild von -Bild von 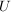 . Das . Das 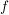 -Bild von -Bild von 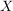 , , 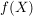 , wird als , wird als  bezeichnet. Für eine Teilmenge bezeichnet. Für eine Teilmenge 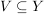 nennt man die Menge nennt man die Menge
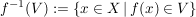
das 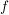 -Urbild von -Urbild von  . Es gelten die folgenden Rechenregeln: . Es gelten die folgenden Rechenregeln:
![$ A,B \subseteq X \ \Rightarrow \ \left\{ \begin{array}{ccc} f(A \cup B) & = & f(A) \cup f(B)\\[5pt] f(A \cap B)& \subseteq & f(A) \cap f(B) \end{array} \right. $ $ A,B \subseteq X \ \Rightarrow \ \left\{ \begin{array}{ccc} f(A \cup B) & = & f(A) \cup f(B)\\[5pt] f(A \cap B)& \subseteq & f(A) \cap f(B) \end{array} \right. $](/teximg/0/4/00434440.png)
![$ U,V \subseteq Y \ \Rightarrow \ \left\{ \begin{array}{ccc} f^{-1}(U \cup V) &= & f^{-1}(U) \cup f^{-1}(V)\\[5pt] f^{-1}(U \cap V) & = & f^{-1}(U) \cap f^{-1}(V) \end{array} \right. $ $ U,V \subseteq Y \ \Rightarrow \ \left\{ \begin{array}{ccc} f^{-1}(U \cup V) &= & f^{-1}(U) \cup f^{-1}(V)\\[5pt] f^{-1}(U \cap V) & = & f^{-1}(U) \cap f^{-1}(V) \end{array} \right. $](/teximg/1/4/00434441.png)
Quelle: isbn3446130799
Mögliche Eigenschaften spezieller Abbildungen
;additiv:
;alternierend (siehe Determinantenfunktion):
;biholomorph:
;bijektiv:
;bilinear:
;differenzierbar:
;epimorph:
;gleichmäßig stetig:
;holomorph:
;homomorph:
;idempotent:  heißt idempotent heißt idempotent  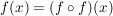 für alle für alle  bzw. bzw.  für alle für alle 
;identisch:
;injektiv:
;integrierbar:
;isomorph:
;komplexwertig:
;konstant:
;leer:
;linear:
;multilinear:
;offen:
;reellwertig:
;selbstähnlich:
;semilinear:
;sequilinear:
;stetig:
;stetig differenzierbar:
;surjektiv:
;symmetrisch:
;umkehrbar:
|