Steckbriefaufgaben
(1) Der Punkt  ist Schnittpunkt mit der x-Achse/ ist Schnittpunkt mit der x-Achse/ 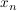 ist Nullstelle ist Nullstelle 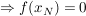
(2) Der Punkt 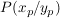 liegt auf dem Graph der Funktion/ist Punkt der Funktion liegt auf dem Graph der Funktion/ist Punkt der Funktion 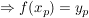 . .
(3) Der Punkt 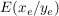 ist Extrempunkt ist Extrempunkt 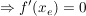 und und 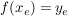 . .
( ist Extremstelle ist Extremstelle 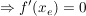 ) )
(4) Der Punkt 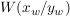 ist Wendepunkt ist Wendepunkt 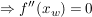 und und 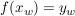 . .
(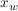 ist Wendestelle ist Wendestelle  ) )
(5) Der Punkt  ist Sattelpunkt/Terassenpunkt ist Sattelpunkt/Terassenpunkt 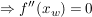 und und 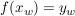 und und 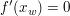 . .
(6) Der Punkt 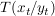 hat eine Tangente mit Steigung hat eine Tangente mit Steigung 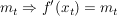 und und 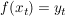 . .
(7) Der Punkt  hat eine Normale mit der Steigung hat eine Normale mit der Steigung 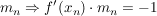 und und  . .
(8) Die Kurven  und und 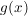 berühren sich in berühren sich in 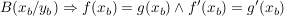 . .
(9) Im Punkt 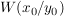 findet man einen Wendepunkt mit waagrechter Tangente: findet man einen Wendepunkt mit waagrechter Tangente:
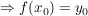 und und 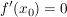 und und 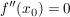 . .
(10) Der Graph der Funktion ist symmetrisch:
- punktsymmetrisch zu
 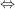 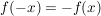
- achsensymmetrisch zur y-Achse
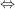 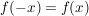
Beispiel:
(1)  ist Extrempunkt: ist Extrempunkt:
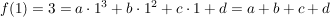 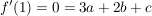
(2) 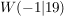 ist Wendepunkt: ist Wendepunkt:
 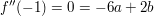
Damit ergibt sich ein Gleichungssystem aus 4 Gleichungen mit 4 Unbekannten, das nach 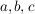 und und 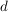 aufzulösen ist: aufzulösen ist:
Ergebnis: 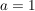 , ,  , , 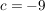 und und 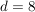
Also lautet die Funktionsgleichung:
Bei dieser Art von Aufgaben kann (und sollte!) man stets eine Probe mit den Originalbeschreibungen im Text der Aufgabe machen, um Rechenfehler bei der Aufstellung der Gleichungen überprüfen zu können!
weitere Aufgaben zum Üben findet man hier
siehe auch Ortskurve, Funktionen aus Eigenschaften
|