OrtskurveDefinition Ortskurve
Schule
... ist die Bezeichnung für einen Funktionsgraphen, der besondere Punkte einer Funktionenschar verbindet.
Beispiel 1:
Durch diese Funktionenschar werden Parabeln in der Scheitelpunktform beschrieben, die sich durch ihre Lage unterscheiden:
je nach Wahl von t ist die Normalparabel nach links (t>0) oder rechts (t<0) verschoben.
Da alle Scheitelpunkte S(t|-2) stets die Ordinate 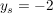 haben, bildet die Gerade y = -2 die Verbindungslinie aller Scheitelpunkte, also die Ortskurve der Scheitelpunkte. haben, bildet die Gerade y = -2 die Verbindungslinie aller Scheitelpunkte, also die Ortskurve der Scheitelpunkte.
Beispiel 2:
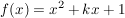 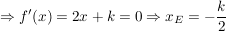
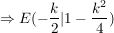
Hier ist nun das k ziemlich "überflüssig", man "eliminiert" es einfach:
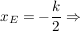 k = -2x ; eingesetzt in den y-Wert k = -2x ; eingesetzt in den y-Wert 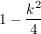 ergibt: ergibt:
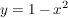
Damit ist der funktionale Zusammenhang zwischen x_E und y_E beschrieben:
die Extrempunkte wandern für alle  auf der angegebenen Kurve. auf der angegebenen Kurve.
Universität
![Link auf "http://de.wikipedia.org/wiki/Kurvenschar" [link]](/images/popup.gif) in Wikipedia in Wikipedia
|