ParabelDefinition Parabel
... heißt der Graph einer quadratischen Funktion.
einfaches Beispiel: die Normalparabel
allgemein:
Diesem Term sieht man allerdings nicht an, wie die Parabel im Koordinatenkreuz liegt.
Daher formt man den Term um, so dass man leicht den Scheitelpunkt ablesen kann.
Zunächst klammert man den Faktor a aus:
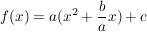
Sodann sucht man zu dem Term in der Klammer die quadratische Ergänzung:

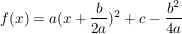
Jetzt liest man ab:
Der Scheitelpunkt hat die Koordinaten: 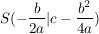
Mit 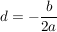 und und 
kann man die Scheitelpunktform einer Parabel also so schreiben:
|