| Mach mit! und verbessere/erweitere diesen Artikel! | | Artikel • Seite bearbeiten • Versionen/Autoren | Formeln IntegralrechnungWichtige Formeln der Integralrechnung
(Für genaue Voraussetzungen, Beweise und Beispiele rufe die einzelnen Artikel auf.)
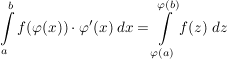 mit 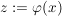
Einige konkrete Stammfunktionen
| | Erstellt: Di 31.08.2004 von Marc | | Letzte Änderung: Sa 31.03.2007 um 15:02 von nsche | | Weitere Autoren: informix, Loddar | | | Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext |
|