FaltungFaltung
Unter einer Faltung versteht man eine multiplikative Operation auf Objekten 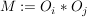
Die kleinste Einheit, die gebildet werden kann ist eine Abbildung  z.B. mit z.B. mit 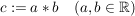
Seien 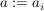 und und  beliebige Folgen, so ist eine neue Folge beliebige Folgen, so ist eine neue Folge 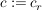 , die aus dem Produkt , die aus dem Produkt  gebildet wurde ein Faltungsprodukt. gebildet wurde ein Faltungsprodukt.
Satz: Seien die Reihen  und und  absolut konvergent, so konvergiert auch die Reihe absolut konvergent, so konvergiert auch die Reihe 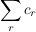 absolut und es gilt: absolut und es gilt:

Faltungsintegral
Das Integral 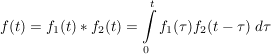 heißt Faltungungsintegral heißt Faltungungsintegral
Eigenschaft der Faltung
Kommutativität
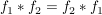
Beweis

Substitution: 

Assoziativität
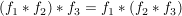
Beweis
![$ [f_1(t)*f_2(t)]*f_3(t)=f_1(t)*[f_2(t)]*f_3(t)] $ $ [f_1(t)*f_2(t)]*f_3(t)=f_1(t)*[f_2(t)]*f_3(t)] $](/teximg/1/7/00475871.png)
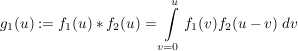
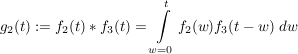
zu zeigen: 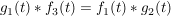

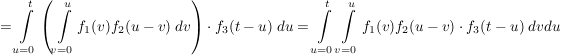



Distributivität

Beispiele:
E-Funktion

es ist: 
wir beginnen mit der rechten Seite
Es seien die beiden Folgen:  und und 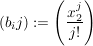 gegeben gegeben
dann ist
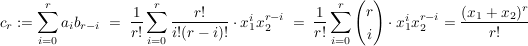
|