Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| www.matheraum.de
Algebra 1
Aufgabenblatt 1
Abgabe: Sa 10.03.2012 13:00 | 03.03.2012 | | Die Aufgabenstellungen erfolgen im Bezug auf das Buch "Algebra" von Karpfinger; gestellt werden Sie von Blackwolf1990 und bis sich ein hilfsbereiter Kursleiter findet wird die Korrektur von Interessenten erbeten. | | Das Thema dieses Aufgabenzettels ist das Kapitel 1: Halbgruppen. | | Aufgabe 1 | I-1: Untersuchen Sie die folgenden inneren Verknüpfungen 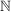 x x 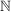 -> -> 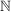 auf Assoziativität, Kommutativität und Existenz von neutralen Elementen: auf Assoziativität, Kommutativität und Existenz von neutralen Elementen:
a) (m,n) 
b) (m,n)  kgV(m,n) kgV(m,n)
Untersuchen Sie, wie viele verschiedene innere Verknüpfungen es auf eine Menge mit 3 Elementen gibt. | | Aufgabe 2 | I-2: Mit welcher der folgenden inneren Verknüpfungen  : : 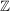 x x 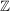 -> -> 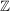 ist ist 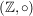 eine Halbgruppe? eine Halbgruppe?
a) x  y = x y = x
b) x  y = 0 y = 0
c) x  y = x - y - xy y = x - y - xy | | Aufgabe 3 | I-3: Begründen Sie das allgemeine Assoziativgesetz: Die Produke von n  3 Elementen 3 Elementen 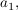 ... , ... , 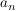 einer Halbgruppe hängen nicht von der Wahl der Klammerung ab. einer Halbgruppe hängen nicht von der Wahl der Klammerung ab. | | Aufgabe 4 | I-4: Es seien die Abbildungen 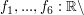 {0,1} -> {0,1} ->  {0,1} definiert durch: {0,1} definiert durch:
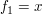 , ,
 , ,
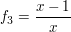 , ,
 , ,
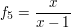 , ,
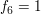 - x . - x .
Zeigen Sie, dass die Menge F aller dieser Funktionen mit der Verknüpfung  : : 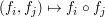 eine Halgruppe mit neutralem Element ist, wobei eine Halgruppe mit neutralem Element ist, wobei 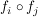 (x) = (x) = 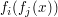 ist. Welche Elemente aus F sind invertierbar? ist. Welche Elemente aus F sind invertierbar? |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|