Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| Lineare Algebra I/II,
Vorkurs, | www.matheraum.de
Lineare Algebra
Aufgabenblatt 2
Abgabe: Mo 13.02.2012 10:00 | 06.02.2012 | | Die Übungsaufgaben beziehen sich auf das Buch "Lineare Algebra" von Gerd Fischer bzw. auf das Inhaltsverzeichnis, das in der Kursbeschreibung zu finden ist. Die Übungsaufgaben (i.d.R. zu immer einem neuen Kapitel im Buch) können bequem in einer Woche gelöst werden. | | Für diese Serie sollten Sie mit folgenden Begriffen vertraut sein: Verknüpfung, Halbgruppe, Gruppe, abelsch, (Links-/Rechts-)Inverses, neutrales Element, Verknüpfungs-/Gruppentafel, Untergruppe, Homomorphismus, Isomorphismus, Zyklische Gruppe, Restklassen modulo m, Repräsentant, Ring, Komplexe Zahlen. | | Aufgabe 1 | II-1: Sei [G,*] eine Gruppe sowie U eine nichtleere Teilmenge von G. Beweisen Sie die Äquivalenz folgender Aussagen:
(i) [U,*] ist Untergruppe von [G,*].
(ii) Für alle a,b 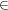 U gilt: U gilt:  U. U. | | Aufgabe 2 | II-2: Zeigen Sie, dass R := {  a,b a,b 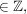 b ungerade } einen kommutativen Ring mit Einselement bildet, der kein Körper ist. b ungerade } einen kommutativen Ring mit Einselement bildet, der kein Körper ist. | | Aufgabe 3 | II-3: Sei [R,+,*] ein Ring mit dem Nullelement 0 (das neutrale Element bez. + in R). Beweisen Sie:
(a) Für alle a 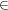 R gilt: 0*a = 0 und a*0 = 0. R gilt: 0*a = 0 und a*0 = 0.
(b) Für alle a,b 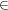 R gilt: (-a)b = -(ab) und a(-b) = -(ab). R gilt: (-a)b = -(ab) und a(-b) = -(ab).
(c) Für alle a,b,c 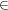 R gilt: (a-b)c = ac - bc und c(a-b) = ca - cb R gilt: (a-b)c = ac - bc und c(a-b) = ca - cb
(d) Für alle a,b 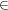 R gilt: (-a)(-b) = ab R gilt: (-a)(-b) = ab | | Aufgabe 4 | II-4: Bestimmen Sie, welche der folgenden Abbildungen Gruppenhomomorphismen sind:
(a) f:  z z  2z 2z
(b) g:  z z  z+1 z+1
(c) h:  z z 
Zusatz: s:  z z  |z| . Ändert sich die Aussage, falls |z| . Ändert sich die Aussage, falls  durch durch  ersetzt wird? ersetzt wird?
Hierbei ist bei den mit * markierten Gruppen die Multiplikation die zugehörige Operation, bei den anderen die Addition. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|