Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Sigrid Sprock
Marc O. Sandlus | www.matheraum.de
Vorbereitung auf das Zentralabitur in Mathematik in NRW
Aufgabenblatt 2
Abgabe: Fr 10.07.2009 16:00 | 06.10.2006 | | Aufgabe 18 | Gegeben sind die Gerade g durch den Punkt P(2 | 1 | -1) und den Richtungsvektor 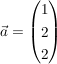 und die Gerade und die Gerade 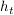 durch den Punkt Q(9 | 12 | -2) und den Richtungsvektor durch den Punkt Q(9 | 12 | -2) und den Richtungsvektor 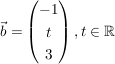 . .
a) Bestimmen Sie t so, dass sich die beiden Geraden schneiden, und berechnen Sie die Koordinaten des Schnittpunktes S.
(Ergebnis: t = -1; S( 6 | 9 | 7) ).
b) Bestimmen Sie die Koordinaten der Punkte auf der Geraden g, die von Q die Entfernung 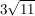 haben. Erstellen Sie dazu eine Skizze. haben. Erstellen Sie dazu eine Skizze.
(Ergebnis: A(6 | 9 | 7) = S, B(4 | 5 | 3) )
c) 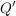 sei der Spiegelpunkt von Q bzgl. der Geraden g. Tragen Sie sei der Spiegelpunkt von Q bzgl. der Geraden g. Tragen Sie 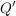 in Ihre Skizze aus Teilaufgabe b) ein und berechnen Sie die Koordinaten von in Ihre Skizze aus Teilaufgabe b) ein und berechnen Sie die Koordinaten von 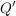 . .
d)
1. Geben Sie eine Koordinatengleichung der durch die Geraden g und 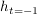 gebildeten Ebene E an. gebildeten Ebene E an.
(mögliches Ergebnis: 8x - 5y + z = 10)
2. Zeigen Sie, dass die Ebene F mit F: x + 2y + 2z = 29 senkrecht auf der Ebene E steht. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|