metrischer RaumDefinition Metrischer Raum
Es sei 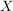 eine nichtleere Menge und es sei eine nichtleere Menge und es sei 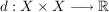 eine Funktion. eine Funktion. 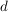 heißt Metrik (auf heißt Metrik (auf 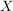 ), falls folgende Bedingungen gelten: ), falls folgende Bedingungen gelten:
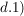 Es gilt Es gilt 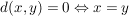 für alle für alle  . (Definitheit) . (Definitheit)
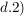 Es gilt Es gilt 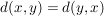 für alle für alle  . (Symmetrie) . (Symmetrie)
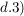 Es gilt Es gilt  für alle für alle  . (Dreiecksungleichung) . (Dreiecksungleichung)
Das Paar 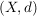 heißt dann metrischer Raum. heißt dann metrischer Raum.
Bemerkungen.
1.) Bei der Definitheit wird oft zusätzlich 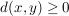 für alle für alle  gefordert. Wir werden aber zeigen, dass darauf verzichtet werden kann, denn: gefordert. Wir werden aber zeigen, dass darauf verzichtet werden kann, denn:
Nach 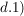 (obige Bedingung!) gilt für alle (obige Bedingung!) gilt für alle  : :
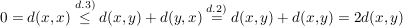 , ,
woraus dann  ( (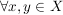 ) folgt. ) folgt. 
2.) Eine Folge 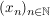 in einem metrischen Raum in einem metrischen Raum 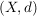 heißt konvergent, falls ein heißt konvergent, falls ein 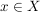 existiert, so dass: existiert, so dass:
Für alle 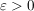 : :  . .
Wir schreiben dann 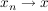 ( (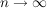 ) und sagen, die Folge ) und sagen, die Folge 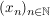 konvergiere gegen den Grenzwert konvergiere gegen den Grenzwert  . .
3.) Ist 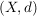 ein metrischer Raum und ist ein metrischer Raum und ist 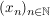 eine konvergente Folge in eine konvergente Folge in 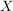 , so ist der Grenzwert von , so ist der Grenzwert von 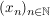 eindeutig bestimmt. eindeutig bestimmt.
Beweis:
Sei  gegeben und seien gegeben und seien  mit mit 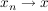 ( (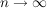 ) und ) und 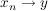 ( (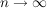 ). ).
Dann existiert ein 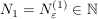 , so dass für alle , so dass für alle 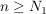 gilt: gilt:
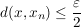 . .
Ebenso existiert ein  , so dass für alle , so dass für alle 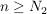 gilt: gilt:
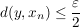 . .
Also gilt für alle 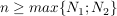 : :
 . .
Da  beliebig war, folgt beliebig war, folgt 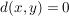 und wegen und wegen 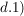 somit somit 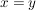 . .
(Denn:
Angenommen, es gelte 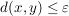 für alle für alle  und es wäre und es wäre  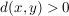 . .
Dann gilt für 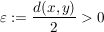 : :
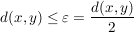 , also: , also:
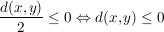 . Da aber auch . Da aber auch 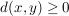 gilt, folgt: gilt, folgt:
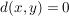 im Widerspruch zu im Widerspruch zu 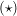 . .  ) ) 
|