PolynomDefinition Polynom
In der Mathematik ist ein Polynom eine Summe von Vielfachen von Potenzen mit natürlichzahligen Exponenten einer Variablen, die in den meisten Fällen mit x bezeichnet wird:
für 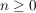 , , 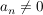 und und 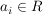 : :
oder kürzer:
Dabei nennt man x die Variable, die reellen Zahlen 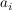 vor den Variablen die Koeffizienten des Polynoms und n den Grad des Polynoms. vor den Variablen die Koeffizienten des Polynoms und n den Grad des Polynoms.
Beispiele
Polynome kommen in einfachster Form schon bei den linearen Funktionen vor: f(x)=3x+4
Wähle 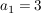 und und 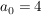 , dann gilt: Polynom vom Grad 1: , dann gilt: Polynom vom Grad 1:
Auch eine quadratische Funktion schreibt man als Polynom vom Grad 2:
Alle ganzrationalen Funktionen haben ein Polynom als Funktionsterm:
Jede Zahl des Dezimalsystems lässt sich in Form eines Polynoms mit x=10 schreiben:
Rechnen mit Polynomen
Die Addition, Subtraktion und Multiplikation zweier Polynome ergibt jeweils wieder ein Polynom:
Die Division zweier Polynome wird nicht immer "aufgehen", es könnte ein "Rest" bleiben.
Dieses untersucht man mit der Polynomdivision.
|