LogarithmusfunktionDefinition Logarithmusfunktion
Schule
... ist diejenige Funktion, die durch die Zuordnung
für alle 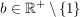 und und 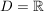 gegeben ist. gegeben ist.
Die Logarithmusfunktion ist als Umkehrfunktion zur Exponentialfunktion mit  definiert. definiert.
Natürliche Logarithmusfunktion
Wählt man als Basis b die Eulersche Zahl e, so bezeichnet man sie durch
Sie ist definiert als die Umkehrfunktion der natürlichen Exponentialfunktion 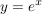 . .
Ableitung und Integral
beliebiger Logarithmus


Natürlicher Logarithmus


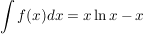
Weblinks
![Link auf "http://de.wikipedia.org/wiki/Logarithmusfunktion" [link]](/images/popup.gif) Logarithmusfunktion bei wikipedia Logarithmusfunktion bei wikipedia
|