IdentitätDefinition Identität
Universität
Sei M eine nichtleere Menge.
Die Funktion 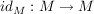 definiert durch definiert durch 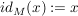 heißt Identität (oder identische Abbildung) auf M. heißt Identität (oder identische Abbildung) auf M.
Beispiele.
1.) Die Funktion 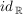 ist die Identität auf ist die Identität auf 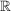 . Es gilt also für alle . Es gilt also für alle 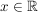 : : 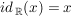 . .
2.) Die Funktion 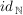 ist die Identität auf ist die Identität auf 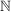 . Es gilt also für alle . Es gilt also für alle 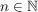 : : 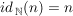 . .
3.) Die Funktion 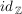 ist die Identität auf ist die Identität auf 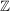 . Es gilt also für alle . Es gilt also für alle 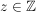 : : 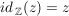 . .
4.) Es gilt beispielsweise: 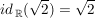 und und 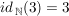 . .
Bemerkungen.
Die Identität auf einer nichtleeren Menge M ordnet jedem Element als Funktionswert genau dasselbe Element zu.
|