Formeln Figuren und KörperFormeln für Figuren und Körper
Figuren
Figuren sind zweidimensionale Gebilde; sie haben einen Flächeninhalt A und einen Umfang U.
allgemeines Dreieck
In jedem Dreieck gilt der Sinussatz, Kosinussatz.
Flächeninhalt: ("Hälfte von Grundseite mal Höhe")
Umfang: (Summe aller Seitenlängen)
Winkel:
(Innenwinkelsummensatz: "Die Summe aller Innenwinkel eines Dreiecks beträgt 180°.")
gleichschenkliges Dreieck
Ein Dreieck, das zwei gleich lange Seiten hat, heißt gleichschenklig.
Äquivalente Definition: Ein Dreieck, das zwei gleich große Winkel besitzt, heißt gleichschenklig.
Die gleich langen Seiten werden Schenkel genannt, die dritte Seite Basis oder Grundseite.
Es sei a die Länge der beiden Schenkel und b die Länge der Basis.
Höhe:
Flächeninhalt:
Umfang:
Winkel:
gleichseitiges Dreieck
Ein Dreieck, dessen drei Seiten gleich lang sind, heißt gleichseitig.
Es sei a die Länge einer (und damit jeder) Seite.
Höhe: (Satz des Pythagoras)
Flächeninhalt:
Umfang:
Winkel:
rechtwinkliges Dreieck
Ein Dreieck, das einen rechten Winkel (90°) besitzt, heißt rechtwinklig.
In rechtwinkligen Dreiecken gilt der Satz des Pythagoras, Höhensatz, Kathetensatz, die Umkehrung des Satz des Thales
Viereck
Winkel: 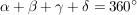
(Innenwinkelsummensatz: "Die Summe aller Innenwinkel eines Vierecks beträgt 360°.")
unregelmäßiges Viereck
Drachen
Trapez
Ein Viereck mit einem Paar von parallelen Gegenseiten nennt man Trapez.
Es seien  und und  die beiden parallelen Seiten. die beiden parallelen Seiten.
Flächeninhalt:
Dabei ist 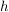 der Abstand der Abstand zwischen den beiden parallelen Seiten der Abstand der Abstand zwischen den beiden parallelen Seiten  und und  . .
Parallelogramm
Ein Viereck mit zwei Paaren von parallelen Gegenseiten nennt man Parallelogramm.
Es seien  eine (Grund)Seite des Parallelogramms und eine (Grund)Seite des Parallelogramms und 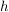 seine Höhe, also der Abstand der Seite seine Höhe, also der Abstand der Seite  von ihrer Gegenseite. von ihrer Gegenseite.
Flächeninhalt:
Raute / Rhombus
Ein Parallelogramm mit vier gleich langen Seiten nennt man Raute oder auch Rhombus.
Rechteck
Ein Parallelogramm, dessen benachbarte Seiten rechtwinklig zueinander sind, nennt man Rechteck.
Flächeninhalt:
Umfang:
Diagonale:
Winkel:
Quadrat
Ein Rechteck, dessen Seiten gleich lang sind, nennt man Quadrat.
Ein Quadrat ist auch eine Raute mit vier rechten Winkeln.
Es sei  die Länge einer (und damit jeder) Seite. die Länge einer (und damit jeder) Seite.
Flächeninhalt:
Umfang:
Diagonale:
Winkel:
n-Eck
regelmäßiges n-Eck
unregelmäßiges n-Eck
Kreis
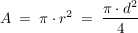
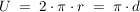
Ellipse
Körper
Prisma
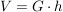
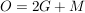
Würfel
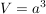
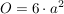
Quader
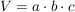
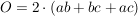
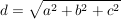 (Raumdiagonale) (Raumdiagonale)
Zylinder
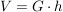
Für senkrechte Zylinder mit einem Kreis als Grundfläche ("Kreiszylinder") gilt weiterhin:
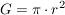
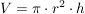
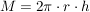
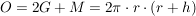
Pyramide
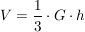
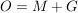
Kegel
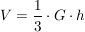
Für senkrechte Kegel mit einem Kreis als Grundfläche ("Kreiskegel") gilt weiterhin:
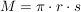
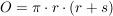
Kugel
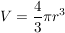
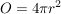
|