FlächeninhaltFlächeninhalt und Integral
Schule
Zwischen dem Flächeninhalt unter einem (stetigen) Funktionsgraphen und dem bestimmten Integral über diese Funktion besteht ein enger Zusammenhang.
Das bestimmte Integral ist zunächst nur für Funktionen f(x)>0 definiert, seine Definition kann jedoch auch für f(x)<0 erweitert werden.
Aus der anschaulichen Herleitung des bestimmten Integrals mit Rechtecken leitet man her, dass der Wert eines bestimmten Integrals, bei dem über dem gesamten Intergrationsintervall f(x)<0 ist, negativ sein muss, weil die "Höhe" der Rechtecke ja durch einen negativen Wert bestimmt ist.
Es gilt also:
Wenn nun die Funktion f im Intervall [a;b] eine Nullstelle  hat, muss man aufpassen: hat, muss man aufpassen:
Beispiel
Nullstelle bei x=1
Das erste Integral liefert einen Wert <0, man spricht von einem orientierten Flächeninhalt, weil die berechnete Fläche unter der x-Achse liegt, hat sie einen negativen Wert.
Will man nun die Fläche zwischen Graph und x-Achse berechnen, darf man nicht 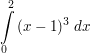 berechnen; es ergäbe sich: berechnen; es ergäbe sich:
weil sich die beiden orientierten Flächenstücke gegenseitig aufheben.
Berechnet man hingegen die beiden Flächen getrennt und betrachtet nur ihren Absolutbetrag, dann erhält man tatsächlich die gewünschte Fläche:
Sind die beiden Flächenstücke unterschiedlich groß, liefert das Integral manchmal sogar einen negativen Wert:
die korrekt berechnete Fläche lautet:
Merkregel:
- Soll das Integral berechnet werden, braucht man sich um Nullstellen im Integrationsintervall nicht zu kümmern.
- Ist dagegen die Fläche gesucht, muss man zunächst die Nullstellen der Funktion im Intervall bestimmen und sich dann von linker Grenze von Nullstelle zu Nullstelle zu hangeln, bis die rechte Grenze erreicht ist.
Universität
TODO
|