AnalytischeGeometrieBitte hier die Aufgabenstellungen sammeln:
Die Gerade 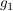 liege in liege in 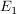 und sei rechtwinklig zur Geraden s. Die Gerade und sei rechtwinklig zur Geraden s. Die Gerade 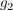 liege in liege in 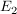 und sei ebenfalls rechtwinklig zur Geraden s. Die Geraden und sei ebenfalls rechtwinklig zur Geraden s. Die Geraden 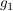 und und 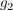 sollen sich in einem Punkt mit der sollen sich in einem Punkt mit der 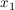 -Koordinate 3 schneiden. Bestimme eine Gleichung von -Koordinate 3 schneiden. Bestimme eine Gleichung von 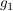 und eine Gleichung von und eine Gleichung von 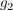 . .
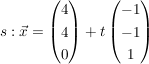
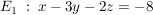
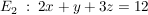
In einem kartesischen Koordinatensystem ist die Schar der Geraden 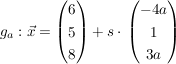 gegeben. gegeben.
Begründen Sie, dass alle Geraden  in einer Ebene in einer Ebene 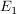 liegen. Stellen Sie eine Gleichung von liegen. Stellen Sie eine Gleichung von 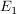 auf. auf.
Gegeben sind die Geraden g: 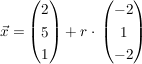 und h: und h: 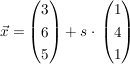 sowie der Punkt P (3 | 3 | 1) sowie der Punkt P (3 | 3 | 1)
Aufgaben:
a) Geben Sie eine Ebenengleichung in Normalenform der Ebene E an, die durch den Punkt P und die Gerade g festgelegt ist.
b) Zeigen Sie, dass die Richtungsvektoren der Geraden g und h zueinander orthogonal sind, die Geraden aber zueinander windschief sind.
|