AdditionstheoremSatz Additionstheoreme
Schule
siehe auch:
![Link auf "http://de.wikipedia.org/wiki/Additionstheorem#Additionstheoreme" [link]](/images/popup.gif) in der Wikipedia in der Wikipedia
mit Erklärung ![Link auf "http://mo.mathematik.uni-stuttgart.de/inhalt/erlaeuterung/erlaeuterung38/" [link]](/images/popup.gif) http://mo.mathematik.uni-stuttgart.de/inhalt/erlaeuterung/erlaeuterung38/ http://mo.mathematik.uni-stuttgart.de/inhalt/erlaeuterung/erlaeuterung38/
oder ![Link auf "http://www.krauseplonka.de/math_onl/ma1/trig_fkt/add_theor1.htm" [link]](/images/popup.gif) http://www.krauseplonka.de/math_onl/ma1/trig_fkt/add_theor1.htm http://www.krauseplonka.de/math_onl/ma1/trig_fkt/add_theor1.htm
Universität
Voraussetzungen und Behauptung
Es gilt für reellwertiges 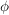 die sogenannte Eulersche Formel die sogenannte Eulersche Formel
wobei man 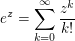 für für 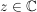 benutzt. Damit ist benutzt. Damit ist 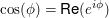 und und 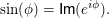
Wegen 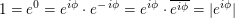 (dabei steht für (dabei steht für 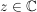 die Zahl die Zahl 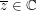 für die konjugiert Komplexe) folgt damit für die konjugiert Komplexe) folgt damit
Bemerkungen.
Weitere Bemerkungen zum Verständnis des Satzes.
Beispiele.
Beweis.
|