AbstandsberechnungenR3Wie berechnet man Abstände im 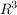 ? ?
Schule
allgemeine Definition
Es seien zwei Punktemengen A und B gegeben (eine Punktemenge kann z.B. ein Punkt, Gerade, Ebene, Kreis, Kugel etc. sein).
Unter dem Abstand d(A,B) der Punktemengen A und B versteht man den kürzesten aller Abstände d(x,y) zweier Punkte mit 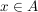 und und 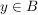 , also , also
Für den Fall, dass A und B abgeschlossen sind (das ist z.B. der Fall, wenn A und B Punkte, Geraden, Ebenen, Kreise, Kugeln sind) gilt:
Im Allgemeinen wird der kürzeste Abstand entlang eines von A auf B gefällten Lotes angenommen; alle im Folgenden aufgeführten Abstandberechnungen beruhen darauf, ein Lot von A auf B zu fällen und die zugehörigen Lotfußpunkte zu berechnen. Der Abstand der Lotfußpunkte ist dann der Abstand d(A,B) der beteiligten Punktemengen.
Konkrete Fälle:
Abstand Punkt-Punkt d(P,Q)
Der Abstand zweier Punkte 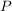 und und 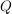 mit den Koordinaten mit den Koordinaten  bzw. bzw.  ist einfach der Betrag bzw. die Norm der Differenz der Ortsvektoren ist einfach der Betrag bzw. die Norm der Differenz der Ortsvektoren  bzw. bzw.  : :
Abstand Punkt-Gerade d(P,g)
Gegeben:  (zugehöriger Ortsvektor (zugehöriger Ortsvektor  ), ), 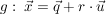
a) Konstruktiv (mit Hilfsebene)
- Stelle eine Hilfsebene E in Normalenform auf, die orthogonal zu g ist und die den Punkt P enthält:
 . .
(Hier konnte einfach der Richtungsvektor 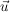 von g als Normalenvektor verwendet werden.) von g als Normalenvektor verwendet werden.)
- Ermittle den Schnittpunkt F der Hilfsebene mit g, durch Einsetzen von g in E. Dies ist der Fußpunkt eines Lotes von P auf g.
- Nun gilt:
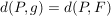 (siehe Abstand Punkt-Punkt) (siehe Abstand Punkt-Punkt)
b) Parameterbestimmung des Lotfußpunktes
Gesucht wird ein Punkt 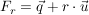 auf der Geraden g mit auf der Geraden g mit 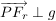 . .
Dies leistet der Ansatz  , nach Auflösen dieser Gleichung nach r: , nach Auflösen dieser Gleichung nach r:

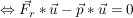

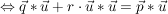
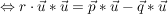
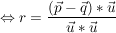
Einsetzen dieses Parameters in 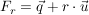 liefert den (Lotfuß-) Punkt liefert den (Lotfuß-) Punkt 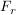
Der gesuchte Abstand 
c) Extremwertaufgabe
Definiere eine Funktion d, die für jeden Parameter r den Abstand des Punktes 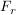 auf der Geraden g von P liefert: auf der Geraden g von P liefert:

d) fertige Formel
Die konstruktive Methode (siehe Teil a) liefert für den 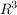 die allgemeine Formel: die allgemeine Formel:
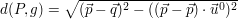 , ,
wobei 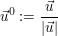 . .
Abstand Punkt-Ebene
Man bestimmt diesen Abstand mit Hilfe der Hesse-Form der Ebenengleichung.
- In gleicher Weise verfährt man beim Abstand zweier paralleler Ebenen und beim Abstand einer Geraden von einer Ebene, die parallel zur Ebene verläuft.
Man wählt dann einfach einen bel. Punkt auf der Ebenen/Geraden und wendet das hier vorgestellte Verfahren an.
Beispiel
Für jede Zahl k ist eine Ebene 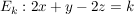 gegeben. gegeben.
Welche der Ebenen  haben vom Punkt P(1|0|-2) den Abstand 12? haben vom Punkt P(1|0|-2) den Abstand 12?
Der Abstand des Punktes P von der Ebene  soll d sein. soll d sein.
Welcher Zusammenhang besteht zwischen der reellen Zahl k und dem Abstand d?
Erst mal gehört k nach links:
Also:  . .
Der Normalenvektor ist demnach:  , ,
seine Länge (wie leicht nachzurechnen) ist 3.
Also musst Du Deine Gleichung durch 3 dividieren:
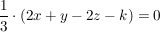
(Für positives k ist das bereits die HNF, für negatives k müsste man zwar mit (-1) multiplizieren, aber das ist überflüssig, weil es nur um den Abstand geht und man folglich sowieso mit Betrag arbeiten muss!)
Nun setze den Punkt ein (und vergiss die Betragsstriche nicht!):
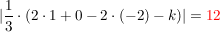 (***) (***)
(Achtung: Statt der 0 steht nun rechts der Abstand, also 12!)
Multipliziere alles mit 3 (damit der Bruch wegfällt)
und rechne die Klammer aus:
|6 - k| = 36
Nun musst Du nur noch diese Betragsgleichung lösen und Du hast die gesuchten Werte für k.
(Zur Kontrolle:  .) .)
Und für den 2. Teil der Aufgabe setze einfach an der Stelle (***) statt 12 den Buchstaben d ein und löse wieder nach k auf. Auch hier ergeben sich 2 Lösungen, die jetzt natürlich von d abhängen.
Abstand Gerade-Gerade
- parallele Geraden
Man wählt einen Punkt auf der ersten Gerade und bestimmt seinen Abstand von der anderen Geraden (wie oben beschrieben).
- windschiefe Geraden
Man stellt eine Ebene E auf, die parallel zu einer der Geraden (h) verläuft und die andere Gerade (g) enthält.
Dann hat jeder Punkt B auf h den gesuchten Abstand von der Ebene E. Der Normalenvektor 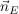 von E ist zugleich der Vektor, der in Richtung des Abstandes zeigt, d.h. er steht auf beiden Geraden senkrecht von E ist zugleich der Vektor, der in Richtung des Abstandes zeigt, d.h. er steht auf beiden Geraden senkrecht
Um nun die Punkte auf beiden Geraden zu finden, die diesen kürzesten Abstand repräsentieren, verfährt man so:
Die Ebene E', die g enthält und in Richtung des Abstandes 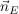 zeigt, schneidet die Gerade h im Punkt zeigt, schneidet die Gerade h im Punkt 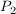 , ,
den zugehörigen Punkt 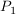 erhält man aus demselben LGS. erhält man aus demselben LGS.
( 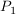 erhält man auch als Schnittpunkt der Lotgeraden erhält man auch als Schnittpunkt der Lotgeraden  mit der Gerade g.) mit der Gerade g.)
Abstand Gerade-Ebene
- parallele Gerade und Ebene
siehe: Abstand Punkt-Ebene
- Gerade nicht parallel zur Ebene
Jede nicht-parallele Gerade schneidet irgendwo die Ebene, also Abstand =0.
Abstand Ebene-Ebene
- parallele Ebenen
siehe: Abstand Punkt-Ebene
- Ebenen nicht parallel zueinander
Nicht-parallele Ebenen schneiden sich irgendwo, also Abstand=0.
Abstand zu einer Kugel - Allgemeines
Gegeben sei eine Kugel 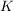 im im 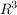 mit Mittelpunkt mit Mittelpunkt 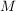 (der Ortsvektor sei (der Ortsvektor sei 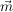 ) und Radius ) und Radius  , also , also 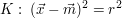 . .
Unter dem Abstand eines Objektes zu einer Kugel versteht man i.A. den Abstand zum Kugelmittelpunkt.
Abstand Punkt-Kugel
a) Abstand zum Mittelpunkt
siehe: Abstand Punkt-Punkt
Es gilt

b) Abstand zur Kugelschale
Liegt der Punkt P außerhalb der Kugel K, so ist der Abstand zur Kugelschale gleich  . .
Abstand Gerade-Kugel
a) Abstand zum Mittelpunkt
siehe: Abstand Punkt-Gerade.
Es gilt:

b) Abstand zur Kugelschale
Ist g eine Passante, also 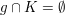 , so ist der Abstand zur Kugelschale gleich , so ist der Abstand zur Kugelschale gleich  . .
Abstand Ebene-Kugel
a) Abstand zum Mittelpunkt
siehe: Abstand Punkt-Ebene
b) Abstand zur Kugelschale
siehe: Abstand Gerade-Kugel (Kugelschale)
Abstand Kugel-Kugel
a) Abstand der Mittelpunkte
siehe: Abstand Punkt-Punkt
b) Abstand der Kugelschalen
siehe: Abstand Gerade-Kugel (Kugelschale)
|