AbleitungAbleitung
Die Funktion f sei auf einem Intervall I definiert und 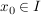 . .
Dann bildet man den Differenzenquotienten
Wenn dieser Differenzenquotient für 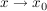 einen Grenzwert hat, einen Grenzwert hat,
so heißt f an der Stelle 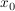 differenzierbar. differenzierbar.
Den Grenzwert nennt man die Ableitung von f an der Stelle 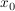
und schreibt 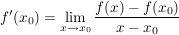 . .
Alternative Schreibweise:
Manchmal ist eine andere Schreibweise hilfreich:
man setzt 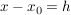 , also , also 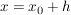
Damit wird der Differenzenquotient zu:
Die Ableitung lautet damit
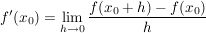 .
Für viele Funktionen gibt es spezielle Ableitungsregeln.
|