ÄquivalenzrelationDefinition Äquivalenzrelation
Schule
Universität
Es sei 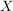 eine Menge. Eine Teilmenge eine Menge. Eine Teilmenge 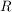 von von  heißt eine Äquivalenzrelation auf heißt eine Äquivalenzrelation auf 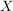 , wenn gilt: , wenn gilt:
 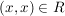 für alle für alle 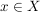 , ,
 aus aus 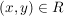 folgt folgt 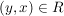 , ,
 aus aus 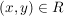 und und 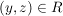 folgt folgt  . .
Die Eigenschaften  , ,  und und  von von 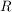 heißen (in gleicher Reihenfolge) reflexiv, symmetrisch und transitiv. heißen (in gleicher Reihenfolge) reflexiv, symmetrisch und transitiv.
Beispiele
a) Sei 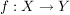 eine Abbildung und eine Abbildung und
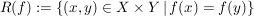 . .
Offensichtlich ist 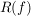 eine Äquivalenzrelation auf eine Äquivalenzrelation auf 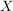 . Der Sonderfall . Der Sonderfall  und und 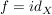 zeigt, dass " zeigt, dass " " eine Äquivalenzrelation definiert, nämlich " eine Äquivalenzrelation definiert, nämlich  . .
b) Für 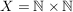 ist ist
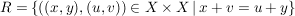
eine Äquivalenzrelation auf 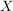 . .
c) Es sei  der Vektorraum der Spaltenvektoren über der Vektorraum der Spaltenvektoren über 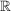 (der Dimension (der Dimension  ). ).

ist eine Äquivalenzrelation auf  . .
d) Es sei  eine Menge von Abbildungen. eine Menge von Abbildungen.
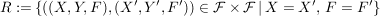
ist eine Äquivalenzrelation auf  . .
Bemerkung:
Sei 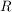 eine Äquivalenzrelation auf einer Menge eine Äquivalenzrelation auf einer Menge 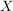 . Anstelle von . Anstelle von 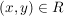 schreibt man oft schreibt man oft 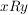 oder oder  oder auch nur oder auch nur  (lies: (lies:  äquivalent äquivalent 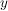 ). ).
In dieser Schreibweise bedeuten die obigen Axiome:
  für alle für alle 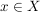 (reflexiv), (reflexiv),
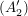 aus aus  folgt folgt  (symmetrisch), (symmetrisch),
 aus aus  und und  folgt folgt 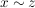 (transitiv). (transitiv).
Zu 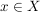 heißt die Teilmenge heißt die Teilmenge
![$ [x]_R:=\{y \in X\, \vert \, (x,y) \in R\} = \{y \in X\, \vert\, x \sim y\} $ $ [x]_R:=\{y \in X\, \vert \, (x,y) \in R\} = \{y \in X\, \vert\, x \sim y\} $](/teximg/1/5/00388151.png)
die Äquivalenzklasse von  (bezüglich (bezüglich 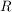 ). Die Menge aller Äquivalenzklassen wird mit ). Die Menge aller Äquivalenzklassen wird mit  bezeichnet: bezeichnet:
![$ X/R:=\{[x]_R\, \vert\, x \in X\} $ $ X/R:=\{[x]_R\, \vert\, x \in X\} $](/teximg/2/5/00388152.png) . .
Die Abbildung 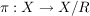 , gegeben durch , gegeben durch ![$ \pi(x) = [x]_R $ $ \pi(x) = [x]_R $](/teximg/4/5/00388154.png) , ist surjektiv und heißt die kanonische Surjektion. , ist surjektiv und heißt die kanonische Surjektion.
Bemerkung:
Die Bedeutung der Äquivalenzrelation liegt darin, dass man Mengen mit einer Äquivalenzrelation in disjunkte Äquivalenzklassen zerlegen kann und ferner, dass Äquivalenz auf 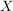 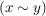 zur Gleichheit zur Gleichheit ![$ ([x]=[y]) $ $ ([x]=[y]) $](/teximg/8/1/00389318.png) in in  führt. führt.
Quelle: isbn3446130799
|